データの実測
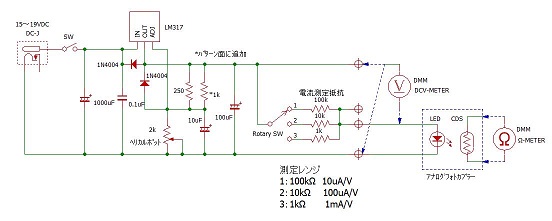 簡 単な定電圧電源キットを使用して左図のような試験回路を作りデータの取得を行いました。入力電流測定範囲は1μA~10mAです。デバイスの入力 に直列抵抗を挿入し、この抵抗の電圧を測定して電流換算します。(抵抗は3段切り替え) 測定電流の設定を容易にするために手持ちのヘリカルポッ トを使用しています。下の写真がが作成したテスト装置です。
簡 単な定電圧電源キットを使用して左図のような試験回路を作りデータの取得を行いました。入力電流測定範囲は1μA~10mAです。デバイスの入力 に直列抵抗を挿入し、この抵抗の電圧を測定して電流換算します。(抵抗は3段切り替え) 測定電流の設定を容易にするために手持ちのヘリカルポッ トを使用しています。下の写真がが作成したテスト装置です。
2台のデジタルテスターを使用して入力電流(I)をパラメーターとして入力電圧(E)、と出力抵抗(R)を 測 ります。(I)は対数を意識して 1,2,3,5,7,10・・・・・・のステップとしました。テスターを見ながら電流を設定し(E)と(R)を実測します。EXCELで測定結果を表にしておきます。
測 ります。(I)は対数を意識して 1,2,3,5,7,10・・・・・・のステップとしました。テスターを見ながら電流を設定し(E)と(R)を実測します。EXCELで測定結果を表にしておきます。
EXCELでこの表を散布図でグラフ化すると分かりやすいです。入力の入力特性すなわちLEDの特性は横軸に入力電圧(E)、縦軸に入力電流 (I)とします。また、出力特性は横軸に入力電流(I)、縦軸に出力抵抗(R)とし、この出力特性は横軸、縦軸ともに対数軸にします。
デバイスモデル作成の準備
基本的な考え方はWebsite “STATIC Spice Model Derivation”を参考にしました。ただし、こ のモデルはあくまで静的なもので、LDR固有の応答速度については考慮されていません。よって使い方としては応答が遅く てもよい回路に限定されてしまいます。私の目的は発振器の振幅制御回路のシミュレーションであり、応答が早いとかえって歪率の低下につながりま す。よって静的モデルで可としました。
実測した入力特性と出力特性を近似式に置き換えてモデルにします。
1)入力特性すなわちLEDの特性を I=exp(E*A-B)・・・・① で近似します。 ①式はLN(I)=E*A-B・・・・②に変形でき ますから、EXCELでLN(I)を計算しておき、この値と実測値(E)を使用してAとBを算出します。変数は2つなので、2点の実測データがあ ればAとBが求められます。 適当な2点の実測を代入し、AとBを計算し、さらに①式を完成させます。 完成した①式をEXCEL上でグラフ化して実測データのグラフと重ね合わせてみます。そうすると 2点の選び方により近似がうまくいっているかよく分かります。何回か試行してできるだけ合致する2点を探し出します。左図はそのグラフですが、実 線が実測値、点線が近似式のグラフです。
2)出力特性を 1/R=exp(LN(I)^2*A+LN(I)*B+C)・・・① で近似します。 ①式はLN(1 /R)=LN(I)^2*A+ LN(I)*B+C・・・②に変形できますから、EXCELで実測データのRからLN(1/R)を計算しておき、この値とパラメータから求める LN(I)を使用して A,BとCを算出します。3点の実測データから求めることが出来ますが、3連の連立方程式を解くのは結構面倒なものです。 EXCELの近似式を使うことにしました。実測データからLN(1/R)を、パラメータの電流(I)も同様にLN(I)を計算しておきます。横軸 にLN(I)を、縦軸にLN(1/R) にしてグラフを描かせます。(左図)近似曲線追加をしますが、ここで近似曲線の書式設定を開き、多項式近似の2次と設定し、さらに“グラフに近似式を表示”にチェックを入 れておきます。左図がそのグラフですが、実線が実測値、点線が近似式を示していますが、重なっています。近似式 y=-0.0612x2-0.3245x- 5.5449が表示されてます。すなわちA=-0.0612、B=-0.3249、C=-5.5449になりました。
A,BとCを①式の変形式、 R=1/(exp(LN(I)^2*A+LN(I)*B+C)に代入してRとIの関係をグラフ化したものが左図で す。青線が実測値、茶線が近似式によるもので、極めて合致しています。
デバイスモデル作成
左図は検証された近似式を使用して忠実にシミュレーター上に記述したもので す。点Aは入力電 圧、点Bは入力電流を(1V=1A)で換算した電圧で入力電流相当がR1に流れます。、点CはこれのLN、R2のR値は近似式通りです。このまま では入力に電流が流れないので、 B3を付加してあります。B3の電流はR1と同じで入力電流が流れます。
このLCR0203.ASCのファイルをサブサーキットとして使用すればシミュレーションが可能になります。ちょっと使いにくいの で、.subcktの形にすることを考えました。LTSpiceでこのLCR0203.ASCを開いて、<VIEW><SpiceNetList> をクリックすると左図のようにNetListが表示されます。このNetListをそのまま利用して.subcktの形にしたものが下記になりま す。
.subckt LCR0203 1 2 3 4
R1 B 0 1
B1 0 B I=exp(V(A)*15.0496-33.6358)
E1 A 0 1 0 1
B2 C 0 V=LN(V(B))
R2 3 0 R=1/(exp(V(C)*(-0.0612*V(C)-0.3249)-5.5449))
V1 1 0 1
V2 3 0 1
B3 1 0 I=V(B)
.ends
同じ手法で作成したMI0202CLのサブサーキットは下記です。
.subckt MI0202CL 1 2 3 4
R1 B 0 1
B1 0 B I=exp(V(A)*23.0607-44.6134)
E1 A 0 1 0 1
B2 C 0 V=LN(V(B))
R2 3 0 R=1/(exp(V(C)*(-0.0903*V(C)-0.3441)-5.1784))
V1 1 0 1
V2 3 0 1
B3 1 0 I=V(B)
.ends
デバイスモデルの検証
上図は作成したデバイスモデルをシミュレーター上で、特性を測ったものです。左が入力特性、右が出力特性ですが、実測した特性と極めて合致して いることが視覚的に分かります。
補足
そもそも、実測曲線から2つの近似曲線が得られる物理・物性的あるいは数学的な根拠は分かっていません。Website “STATIC Spice Model Derivation”で記載されていたのを試してみた結果、予想以上に近似されていることが分かりました。このWebsiteの著者に御礼申し上げます。
このモデルは先に書いたように、応答時間について考慮されていませんし、一つのサンプルから作成したものなので、代表特性になっているか どうかも分かりません。 これらをご理解いただく前提でLT Spicce上で使用できるLCR0203およびMI0202CLのデバイスモデルを公開しました。